卡特兰数又称卡塔兰数 (Catalan Number),是组合数学中一个经常出现在各种计数问题中的数列。其前几项为：
1 |
公式
求卡特兰数列的第n项
公式1
$$
f(n)=\sum_{i=0}^{n-1}f(i)\times f(n-i-1)
$$
公式2
$$
f(n)=\frac {f(n-1)\times(f\times n-2)}{n+1}
$$
公式3
$$
f(n)=\frac{C_{2n}^{n}}{n+1}
$$
公式4
$$
f(n)=C_{2n}^{n}-C_{2n}^{n-1}
$$
应用
卡特兰数经常出现在OI以及ACM中，在生活中也有广泛的应用。
进出栈问题
栈是一种先进后出（FILO,First In Last Out）的数据结构
那么一个足够大的栈的进栈序列为1,2,3,⋯,n时有多少个不同的出栈序列？
假设k为最后一个出栈的元素。比k早进栈且早出栈的有k-1个数，一共有f(k-1)种方案。比k晚进栈且早出栈的有n-k个数，一共有f(n-k)种方案。所以一共有f(k-1)*f(n-k)种方案。当k取不同值时，产生的出栈序列是互相独立的，因此可累加。因为k的取值范围是1~n，所以结果为
$$
f(n)=f(0)\times f(n-1)+f(1)\times f(n-2)+…+f(n-1)\times f(0)
$$
注意：n>=2
例题：P1044 栈
long long f[N]; |
二叉树的计数
已知一颗二叉树有n个结点，问：该二叉树能组成多少种不同的形态?
假设如果采用中序遍历的话，根结点第k个被访问到，则根结点的左子树有
k-1个点、根结点的右指数有n-k个点。k的取值范围为1到n。明显的卡特兰数。
AB排列问题
有n个A和n个B排成一排，从第1个位置开始到任何位置，B的个数不能超过A的个数，这样的排列有多少种？
如：
n=1: AB
n=2: AABB ABAB
n=3: AAABBB AABABB AABBAB ABAABB ABABA
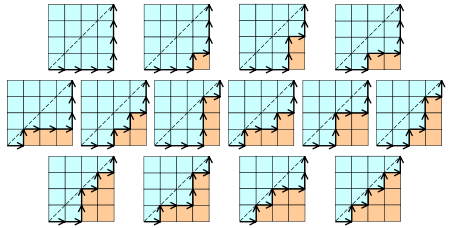
在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少种走法？
向右走相当于进栈(A)，向左走相当于出栈(B)，本质就是n个数出栈次序的问题。
乘法加括号
NOI 1988
对于连乘：
$$
a[0]\times a[1]\times a[2]\times …\times a[n]
$$
加了括号后可以改变它的运算顺序，问有多少种不同的运算顺序？
将其表示成一颗二叉树，把
*逐个作为根，得到卡特兰数。
参考文献&网址
- <信息学奥赛之数学一本通>林厚从 主编, 东南大学出版社
- https://blog.csdn.net/wookaikaiko/article/details/81105031
- https://www.luogu.org/blog/Ning-H/solution-p1044
,是组合数学中一个经常出现在各种计数问题中的数列。其前几项为：
1251442132429143048621679658786208012742900...)
,是组合数学中一个经常出现在各种计数问题中的数列。其前几项为：
1251442132429143048621679658786208012742900...)
,是组合数学中一个经常出现在各种计数问题中的数列。其前几项为：
1251442132429143048621679658786208012742900...)